Sequences and Series - Advanced

A series in which each term is formed by multiplying the corresponding terms of an A.P. and G.P. is called Arithmetico Geometric series. It is more popularly known as an A.G.P.
The general or standard form of such a series is a, (a +d) r, (a +2 d) r² and so on.

Sum of infinite number of terms of an A.G.P with |r| < 1 is

S∞ =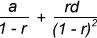

Where,
a = first term
d = common difference of A.P. 
r = common ratio of G.P.

Standard Series

• The sum of first n natural numbers
  = ∑ n = 1+ 2 + 3 + 4 +....+ n = 
• The sum of squares of first n natural numbers
  = ∑ n² = 1² + 2² + 3² +....+ n² = 
• The sum of cubes of the first n natural numbers
  = ∑ n³ = 1ˆ3 + 2ˆ3 + 3ˆ3 + 4ˆ3 +……+ nˆ3 = 
• Sum of first n odd natural numbers = 1+ 3 + 5 +......+ up to n terms = nˆ2.
• Sum of first n even natural numbers = 2 +4 + 6 +......+ up to n terms = n (n+1).
• For any series T_n = S_n – S_n-1
• Fibonacci Series-In Fibonacci series, each term is the sum of previous two terms i.e.
  F (n+1) = Fn + F (n-1) where n, n+1 and n-1 represent the term number).
  Example: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233.....

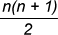
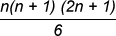
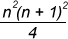
Method of Differences:

In some series, the differences of successive terms (T_n and T_n-1) is helpful in calculating the sum of the series. This method can be applied when the differences between the two consecutive terms is in A.P. Let us see how we can apply this method to questions.

Example: Find the sum to infinity of the series 1² + 2². x + 3².x² + 4².x³ +...,.... |x| < 1.

Solution: Though the given series is not an Arithmetico-Geometric series, however, the differences (2² - 1²), (3² - 2²) , .....form an AP. So, we can use the Method of Differences.

Let S = 1 + 4x + 9x² +16x³ +.... ∞. 
Multiply both sides with common ratio x of the GP.
Sx = x + 4x² + 9x³ +......∞. 
Now, subtract the two equations.
=> (1 – x) S = 1 + 3x + 5x² + 7x³ +....∞ ....... (1)
Now, let R = 1 + 3x + 5x² + 7x³ +...∞, which is an Arithmetico-Geometric series with a = 1, d = 2 and r = x.

For an A.G.P, 
Sum R =  ,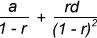
Substituting the values, we get R =  ,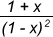
Substitute R in (1), we get, 
(1 – x) S =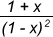 
⇒ S = ,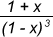

Solved Examples:

Example 1: Evaluate 1 + 4/5 + 7/5² + 10/5³ +..... to infinite terms.

Solution: Here, the series is an A.G.P, where 1, 4, 7, 10...... is an AP, with a = 1 and d = 3 and 1, 1/5, 1/5²,..... is a GP, with r = 1/5.
For an A.G.P., S∞ =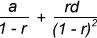  
By putting the values, we get S∞ = 35/16.
Hence, answer=35/16.

Example 2: Find the sum of the series 2.5+5.8 +8.11 +... upto n terms.

Solution: This series is formed by multiplying the corresponding terms of sequences 2, 5, 8 ... and 5, 8, 11 ... both of which are A.P.s.
Now, nth term of first A.P. = 2 + (n – 1)3 = 3n – 1. 
nth term of second A.P. = 5 +(n – 1)3 = 3n +2.
Hence, nth term of the given series, T_n = (3n – 1) (3n +2) = 9n² +3n – 2.
Thus, the required sum, 
S_n = ∑Tn = &sum(9 n² +3n – 2) 
= 9∑ n² + 3∑n - ∑2 = 9∑ n² + 3∑n – 2n.
⇒ 9 × n (n + 1) (2n + 1)/6 + 3 × n (n + 1)/2 - 2n.
= n (3n² +6n +1)
Hence, answer= n (3n² +6n +1)

Example 3: Find the sum of the following series: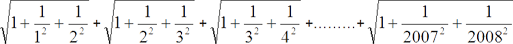

Solution: There are 2007 terms in the given sequence and we want to evaluate S2007. Here, we will apply a shortcut called interpolation.
S₁ = T₁ =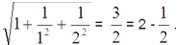 
S₂ = T₁ + T₂ = 

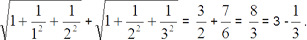
On interpolating, we can say S3 = 4 - 1/4, S₄ = 5- 1/5....so on.
Continuing the same logic S₂₀₀₇ = 2008 - 1/2008.

CAT 2017 Solved Question:

Question:

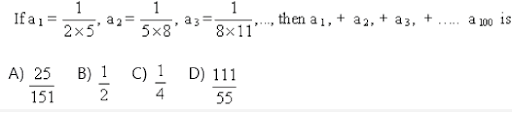
Solution:

Key Learning:

• The method of differences can be applied when the differences between the two consecutive terms is in A.P.
• For any series T_n = S_n – S_n-1
• The standard series given in the article find application in almost every topic in mathematics.
• The method of interpolation finds its application in many questions of sequences and series