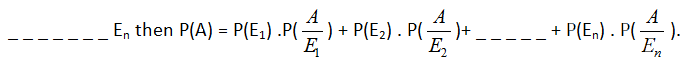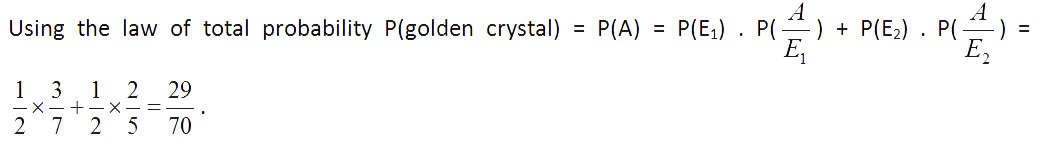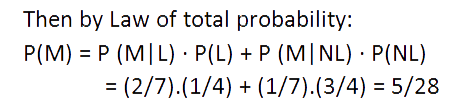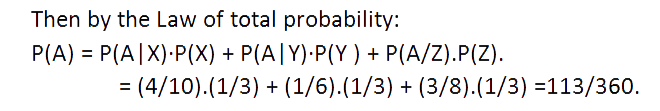Welcome to this lesson on CAT probability. In this article, we cover the important aspects for this topic and understand the key things that you should keep in mind. By adopting a step-wise approach and covering different aspects.
To solve questions of probability, one should be fully aware of the concepts of permutation and combination. It is not a difficult nut to crack. CAT questions on these topics are generally logical in nature. One needs to brush up his basics of Permutation and combination to master this area. Also, one should know the following related to the concepts of probability:
Thus P(A/B ) = Probability of occurrence of A under the condition that B has already occurred.
3. Let S be the sample space and let E1, E2, _ _ _ _ En be n mutually exclusive and exhaustive events associated with a random experiment. If A is any event which occurs with E1 or E2 or
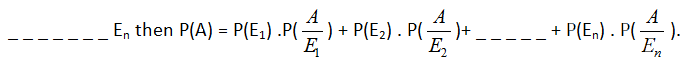
4. Let S be the sample space and let E1, E2, _ _ _ _ _ En be n mutually exclusive and exhaustive events associated with a random experiment. If A is any event which occurs with E1 or E2, _ _ _ _ or En.
5. All Venn diagram formulas hold good for probability questions as well.
CAT Probability Examples:
Example 1: An urn contains 10 white and 15 black balls. Two balls are drawn in succession without replacement. What is the probability that first is white and second is black?
Solution: Let A = Getting a white ball in the first draw and B = Getting a Black Ball in the second draw. Required Probability = Probability of getting a white ball in the first draw and a black ball in
Example 2: A standard die is rolled. Let C be the event that the outcome is an odd number and D be the event that the outcome is not more than 3. Find the probability C knowing that D has happened?
Solution: Let's find the conditional probability of C given that D has occurred.
If we know D has occurred, the possible outcomes are {1,2,3}.
For C to happen the outcome must be in C∩D={1,3}.
P(C|D) = P(C∩D)/P(D) = 2/3
Example3: Hunar wrote two sections of CAT paper ; Verbal and QA in the same order. The probability of her passing both sections is 0.6. The probability of her passing the verbal section is 0.8. What is the probability of her passing the QA section given that she has passed the Verbal section?
Solution: Let P(QA) = passing QA’s section and P(V) = passing Verbal section. So, P(QA/V) = P(QA∩V)/P(V) = 0.6/0.8⇒0.75
Example 4: Amika has 2 pouches. One pouch contains 3 golden and 4 silver crystals. The second pouch contains 2 golden and 3 silver crystals. One pouch is selected at random and from the selected pouch, one crystal is drawn. Find the probability that the crystal drawn is golden.
Solution: Since one of the two pouches is selected randomly, So,P(E1) =1/2 and P(E2) = 1/2 .
Now P(A/E1) = Probability of drawing a golden crystal when the first pouch has been chosen =3/7 and P(A/E2)=Probability of drawing an golden crystal when the second pouch has been selected = 2/5
Example 5: A year is selected at random. What is the probability that it contains 53 Mondays if every fourth year is a leap year?( It is a very famous question and appears frequently in many competitive exams.)
Solution: Let P(L) = probability of selecting a leap year. P(NL) = probability of selecting a non - leap year. P(M) = probability of getting 53 Mondays in a year.
Example 6: There are three cartons, each containing a different number of soda bottles. The first carton has 10 bottles, of which four are flat, the second has six bottles, of which one is flat, and the third carton has eight bottles of which three are flat. What is the probability of a flat bottle being selected when a bottle is chosen at random from one of the three cartons?
Solution: Let A be the event that the selected bottle is flat, X be the event that it is chosen from carton 1, Y be the event that it is chosen from carton 2, Z be the event that it is chosen from carton 3.
CAT Quantitative Aptitude: Preparation Articles
-thumbnail_0.png?null&itok=Xhd6gz54 "CAT Formulae Book")
-thumbnail.png?null&itok=USokav20)
-thumbnail.png?null&itok=B9Rsz-Xq)
