We all have encountered a frequently asked question, "How many squares are there in a 8*8 chessboard?"
We usually think the answer is 8*8=64, right?
But in this case we have just counted 1*1 squares. What about the 2*2 squares, 3*3 squares, 4*4 squares and so on?
Number of 1*1 squares= 8*8=64
Number of 2*2 squares= 7*7=49
Number of 3*3 squares= 6*6=36
Number of 4*4 squares= 5*5=25
Number of 5*5 squares= 4*4=16
Number of 6*6 squares= 3*3=9
Number of 7*7 squares= 2*2=4
Number of 8*8 squares= 1*1=1
Total number of Squares= 82+72+62+...+22+12= 204
Can you see a pattern?
In a 8*8 chessboard, the total number of squares is ∑82
We can generalize this in the following way:
Now let us calculate the number of rectangles in 8*8 chessboard.
A rectangle can have the following dimensions: 1*1, 1*2, 1*3, 1*4… 1*8, 2*2, 2*3, 2*4, …2*8, 3*3, 3*4, ….7*8, 8*8.
We can approach the problem in the following way:
To form a rectangle, we need 4 lines. (2 sets of parallel lines). We can select these lines by = 9C2 * 9C2 = 36*36=1296.
We can generalize this in the following way:
Total number of rectangles in a n*n chessboard will be
= n+1C2*n+1C2
Note: The squares will also be included in counting rectangles.
Calculating it every time is cumbersome. Also, we can be asked to calculate the number of squares and rectangles in a m*n board. In this case, the above-derived formulas won't work.
Having a standard formula to calculate the number of squares and rectangles in an m*n chessboard will simplify the problem.
Let us see how we can get a generalized formula to calculate the number of squares and rectangles in an m*n chessboard.
In a m*n board,
Total number of rectangles in a m*n board
= m+1C2*n+1C2
(A rectangle can be formed by selecting 2 lines from m+1 lines and 2 lines from n+1 lines) For example, number of rectangles in a 2*3 board will be =18
Total number of squares in a m*n board= ∑ (m*n); m, n varying from 1 to m,n respectively.
For example, number of squares in 2*3 board = 2*3+1*2=8
For your practice, you can calculate the number of squares and rectangles in a 6*7 board.
Let's solve some examples based on this concept.
Example 1: In how many ways can you place 2 rooks on 8*8 chessboard such that they are not in attacking positions?
Solution:
Number of ways of selecting 1st rook= 64C1
Number of ways of selecting 2nd rook (it should not be in the same row or column) =7*7/2
Therefore, total number of ways= 64*7*7/2= 32*49=1568.
Example 2: If two squares are chosen on a 8*8 chessboard, what is the probability that they have one side in common?
Solution:
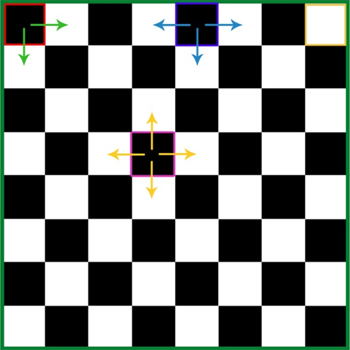
To count the favourable cases, we will consider 3 cases.
Case 1: The corner squares.
There are 4 corner squares. For each corner square, we can select the other square in 2 ways.
Therefore, for this cases, favourable cases= 4*2=8
Case 2: The squares on the edges.
There are 24 squares on the edges. For each such square, we can select the other square in 3 ways.
Therefore, for this cases, favourable cases= 24*3=72
Case 3: The inner squares.
There are 36 inner squares. For each such square, we can select the other square in 4 ways.
Therefore, for this case, favourable cases= 36*4=144
On adding these three cases we get 8+72+144=224
But this is not the final answer.
We have counted every case twice.
So total favourable cases= 224/2=112
The probability= 112/2016
Example 3: If two squares are chosen on a 8*8 chessboard, what is the probability that they have one vertex in common?
Solution:
Total number of ways of selecting 2 squares= 64C2= 2016
To count the favourable cases, we will consider 3 cases.
Case 1: The corner squares.
There are 4 corner squares. For each corner square, we can select the other square in 1 ways.
Therefore, for this cases, favourable cases= 4*1=4
Case 2: The squares on the edges.
There are 24 squares on the edges. For each such square, we can select the other square in 2 ways.
Therefore, for this cases, favourable cases= 24*2=48
Case 3: The inner squares
There are 36 inner squares. For each such square, we can select the other square in 4 ways.
Therefore, for this cases, favourable cases= 36*4=144
On adding these three cases we get 4+48+144=196
But this is not the final answer.
We have counted every case twice.
So total favourable cases= 196/2=98
The probability= 98/2016.
Remember the formulas to calculate the number of squares and rectangles in a m*n board. It can be directly applied to questions on chessboard.
_1.jpg?null)
-thumbnail_0.png?null&itok=Xhd6gz54 "CAT Formulae Book")
-thumbnail.png?null&itok=USokav20)
-thumbnail.png?null&itok=B9Rsz-Xq)
