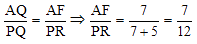Geometry forms an essential part of Quant section in CAT, XAT and other MBA entrance tests. It can be the easiest topics of Quantitative Aptitude, if you prepare it well. Like any other topic, geometry too needs a lot of practice. In this article, we will discuss about polygons and its important properties. The important properties and formulas discussed in this article find direct application in questions. So, make sure you go through this article in detail.
Polygon: A polygon is a closed plane figure formed by three or more line segments, called the sides of the polygon. Each side intersects exactly two other sides at their endpoints. The points of intersection of the sides are known as vertices. The term "polygon" is used to mean a convex polygon, that is, a polygon in which each interior angle has a measure of less than 180°. The following figures are polygons:
The following figures are not polygons:
| Number of sides | Name of the Polygon |
|---|---|
| 3 | Triangle |
| 4 | Quadrilateral |
| 5 | Pentagon |
| 6 | Hexagon |
| 7 | Heptagon |
| 8 | Octagon |
| 9 | Nonagon |
| 10 | Decagon |
Convex polygon: A polygon in which none of the interior angles is more than 180° is called a convex polygon.
Concave polygon: A polygon in which at least one of the interior angles is more than 180° is called a concave polygon.
Regular polygon: A polygon which has all its sides and angles equal is called a regular polygon.
Perimeter of a polygon: The perimeter of a polygon is the sum of the lengths of all its sides.
Area of a polygon: The region enclosed within a figure is called its area.
Diagonal of a polygon: The segment joining any two non-consecutive vertices is called a diagonal.
Polygon formulas:
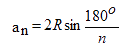where an is the side of regular inscribed polygons, where R is the radius of the circumscribed circle,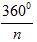
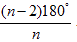
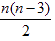
Example: What is the area of a regular octagon of side 8 cm?
Solution: The area of the octagon can be expressed as the difference of the larger square that comprises the octagon and the 4 right triangles at the corners that you can deduct.
Each of the right triangles will have the two perpendicular sides as 8/ √2.
The side of the bigger square will be 8 + 8/√2 + 8/√2 = (1+ √2) 8.
Squaring both sides, we get the area of the square as (1 + 2 + 2√2)82.
The sum of areas of the four triangles = 4 * ½ *(1/√2)2 * 82.
The difference between the two works out to be (2+2√2) * 82, that will be area of the octagon.
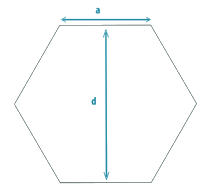
Here, a = side of the hexagon;
d= diameter of the circle inscribed (distance between two parallel sides);
p= perimeter of the hexagon.
The hexagon can be divided into 6 equilateral triangles with side=a
Hence, area of hexagon=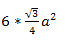 
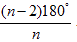
Area of hexagon=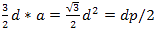 
Length of the diagonals=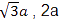
Solved Examples:
Question 1: What is the area of a regular octagon of side a?
Solution: Answer- option 1
The area of the octagon can be expressed as the difference of the larger square that comprises the octagon and the 4 right triangles at the corners that we can deduct.
Each of the right triangles will have the two perpendicular sides as a / √2.
The side of the bigger square will be a + a/√2 + a/√2 = (1 + √2) a.
On squaring we get the area of the square as (1 + 2 + 2√2)a2 and that of 4 triangles as 4 x ½ x(1/√2)2 x a2.
The difference between the two equals (2+2√2) x a2.
Question 2: ABCDEF is a regular hexagon AP: PB = 5: 2 and PR is parallel to AF. Find the ratio of lengths of AF to PR.
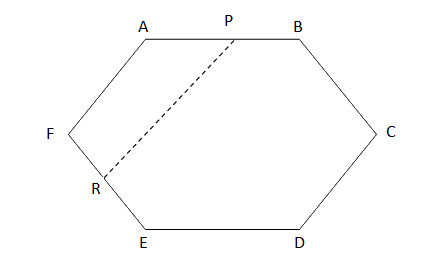
Solution: Answer- Option 3
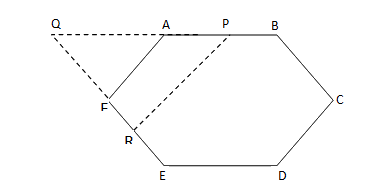
Here, ΔAQF is an equilateral triangle
So AF = AQ
But AF || PR. Then Δ AQF and Δ PQR are similar So 
-thumbnail_0.png?null&itok=Xhd6gz54 "CAT Formulae Book")
-thumbnail.png?null&itok=USokav20)
-thumbnail.png?null&itok=B9Rsz-Xq)
