Syllogisms form an integral part of reasoning. Questions from this topic frequently appear in various MBA entrance exams like CAT, SNAP, IIFT, etc; Bank PO exams and other aptitude tests.
Syllogism is a form of reasoning in which a conclusion is drawn from two or three given propositions or statements. It uses deductive reasoning rather than inductive reasoning. You have to take the given statements to be true, even if they are at a variance from established facts.
Let us see an example of deductive reasoning.
This conclusion is quite visible. But to solve complex problems we have some standard methods.
Following are the four major types of statements generally asked:
| Sr. No. | Type of statement | Represented by the letter | Example |
|---|---|---|---|
| 1 | Universal Positive | A | All boys are handsome |
| 2 | Universal Negative | E | No girl is clever |
| 3 | Particular Positive | I | Some rats are dogs |
| 4 | Particular Negative | O | Some ships are not planes |
While deriving conclusions, following points should be kept in mind:
Another method of solving such type of questions is by drawing Venn diagram representing the statements. However, it is important that all possible Venn diagrams be drawn. If a conclusion can be deduced from all the possible solutions then that conclusion is true. If the conclusion can be concluded from one of the possible Venn diagram and not from the other possible Venn diagram then that conclusion is taken as false.
Example1:Which of the two conclusions can be concluded on the basis of given statements?
Solution: Now, in this case, the possible conclusion is: Some scissors are parrots (I to I), as the universal principal no. 4 says, that with two particular statements only I to I is possible. Therefore, only 1 conclusion is possible. Nothing else is possible.
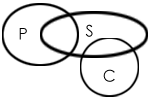
Example 2 : Which of the two conclusions can be concluded on the basis of given statements?
Solution:
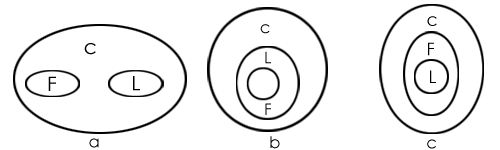
Three possible diagrams are shown above for the given statements.
Conclusion I follows from last two possible solutions, but does not follow from the first possible solution. Therefore, this conclusion is false.
Conclusion II follows from all the three possible solutions.
Therefore, conclusion II is true.
Example 3: Which of the two conclusions can be concluded on the basis of given statements?
Solution: Two possible diagrams are shown below for the given statements.
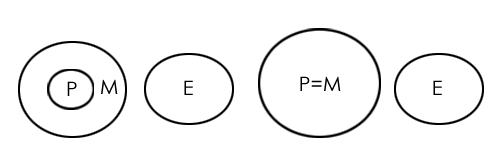
Conclusion I follows from both the possibilities, so conclusion I is true.
Conclusion II also follows from both the possibilities, so conclusion II is also true.
Therefore, both conclusions are true.
Example 4: Which of the two conclusions can be concluded on the basis of given statements?
Solution: Two possible diagrams are shown below for the given statements.
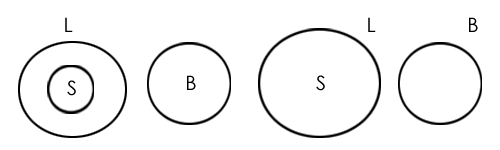
Conclusion I: False (conclusion follows from the second possibility but doesn't follow from the first possibility)
Conclusion II: True (conclusion follows from both the Venn diagram possibilities.)
Therefore, only conclusion II is true.
To know the importance of this topic in various exams, take a look at some previous year CAT questions.
Question 1: The question has a set of four statements. Each statement has three segments. Choose the alternative where the third segment in the statement can be logically deduced using both the preceding two, but not just from one of them.
Solution: Option C
Only C is the correct answer choice. Statement A is invalid. We cannot conclude about 'all YP', but only about 'Some YP' (shaded portion) who are, incidentally, 'all CY'.
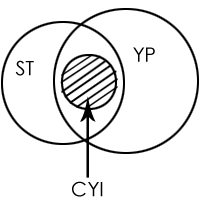
CYI = Citizens of Yes Islands
ST = People who speak only the truth
YP = Young people
Statement C is valid. The 'Some YP' who are CYI also are people who speak only the truth. (Shaded portion)
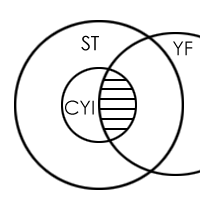
Statement D is invalid, because the 'some people' and the 'some CYI' need not have any relationship between them, just because both speak only the truth.
Question 2: The question has a set of four statements. Each statement has three segments. Choose the alternative where the third segment in the statement can be logically deduced using both the preceding two, but not just from one of them.
Solution: Option B
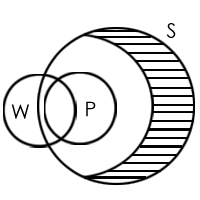
Statement A is invalid, as no definite relationship between P and W can be established.
Note: 'Many' is translated as 'Some' to convert the statement in standard form.
The 'Some S (shared portion)' are not w, but some other S could be W, as shown in the Venn diagram above.
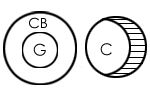
Statement B is valid, as the 'Some C (shaded portion)' that do not climb beans stalks cannot be giants.
G = Giants
C = Chicken
CB = Creatures which climb beanstalks C is invalid, the 'Some penguins' that live in snowdrifts need not be explorers.
D is invalid, as Amar is the tallest among the three, but it is not clear how the heights of Akbar and Anthony are compared.
Note: This is not a 'Categorical' syllogism comprising statements, as such. All S is P, No S is P, Some S is P and Some S is not P. It is a 'relational' syllogism comprising relational statements that normally feature in analytical reasoning. Be alert: CAT examiner is in the habit of jumbling up questions to throw you off gear.
Question 3: Choose an option in which the last statement can be deduced logically from the preceding two. Example:
Solution: Option A) ABC is a valid option, where statement C can be concluded from statements A and B
Question 4: The question has a set of five statements. Each option has three segments. Choose the alternative where the third segment in the statement can be logically deduced using both the preceding two, but not just from one of them
Solution: Option D
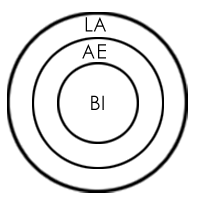
BI = Balram
AE = Ant-eaters
LA = Creatures who like ants
Anteaters like ants and Balram is an anteater.
Therefore, Balram likes ants.
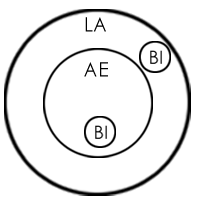
Ant-eaters, creatures who like ants, boys and Balaram
Furthermore, E: 'Balram may eat ants' can never feature in a valid syllogism. A 'may’ statement implies 'may not' and is not always true. Hence, such a statement is of no use to a student of logic, who is concerned with the process of reasoning, arriving at a definite conclusion from definite information given in the premises..