In this article, we cover the important dimensions related to CAT mensuration. All important aspects related to the topic are covered here and you will understand how to approach this topic.
CAT Mensuration: Tips and Tricks
These are four essential points that you need to keep in mind for this topic:
- Practice, practice and more practice: Like any other area, this area too needs a lot of practice. Try to solve as many online CAT mock test/CAT model tests you can and get familiar with the tricks for mensuration.
- Consistency in practice: Students tend to forget the mensuration part that they have done during school times. So key to score good marks in this section is consistency in practice. Spend sufficient time every day practicing quantitative aptitude in general and mensuration in particular for CAT exam. The more you spend time with the problems, the more familiar they will get.
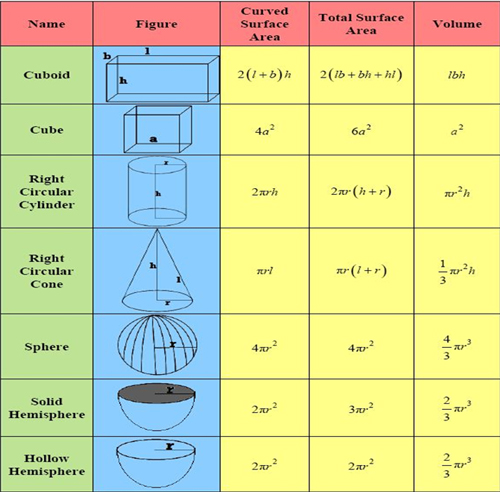
- Importance of Formulas: Learn the mensuration formulas like those for cube, cuboid, cylinder, sphere etc. for CAT as lot of problems can be solved if you have the formula in place. Write the formulas down on a piece of paper and stick it on to the wall where you can see it regularly. It’ll help you to memorize them.
- During Exam: If you get stuck with a mensuration question, don’t waste your time trying to solve it right away. Instead, get on with the others and come back to the question when you are done with the rest of the doable questions.
CAT Mensuration SYLLABUS
Formulas pertaining to Curved Surface Area, Total Surface Area, Volume for solid figures like:
- Cube,
- Cuboid,
- Cylinder,
- Cone,
- Sphere,
- Frustum
- Polygon,
- Prism,
- Pyramid etc.
Important Concepts
- Effect of cavity on the surface area of solid figure,
- Length of longest rod in cubical/cuboid room
- Effect of melting the solids to form new solid
- Slant surface and Whole surface of Pyramid
- Frustum of Pyramid etc.
Frequently used important Mensuration Formulas:
CAT Mensuration Shortcuts
Mensuration in CAT is one of the easiest topics of Quantitative Aptitude, if you spend enough time preparing for it. Aspirants can always use various shortcuts for solving Mensuration questions; some of useful shortcuts are discussed as under:
- Do take Advantage of SYMMETRY: In Mensuration many times a question can be solved with the help of SYMMETRY. Questions involving solid figures like cubes, spheres, pyramid etc. can be solved using the concept of SYMMETRY in an easier manner, but for that a good practice and strong analysis is required.
- Options Elimination: There are certain questions where options can be ruled out one by one instead of forming an option. In such questions we just ensure that all the conditions given in the question must be fulfilled and whichever option satisfies all the conditions it will be our answer. But please remember there should not be “None of these” option in such questions.
- Previous CAT questions: Go through all the previous year's CAT Mensuration questions, as so many questions are based on the concepts, which have appeared in earlier CAT exams.
- Answering questions in percentage: So many times, you have a question in which you have to answer the percentage area wasted. In all those cases, you can avoid the actual values given and take the values, which are more suitable for calculation as it would not affect your answer in percentage.
CAT Mensuration Questions
Q1: The length, breadth and height of a room are in the ratio 3:2:1. If the breadth and height are halved while the length is doubled, then the total area of the four walls of the room will
- 1.Remain the same
- 2.Dec. by 13.64%
- 3.Dec. by 15%
- 4.Dec. by 18.75%
- 5.Dec. by 30%
Solution: In the present case, let Length = l = 3x, Breadth = b = 2x, Height = h = x
Then, Area of four walls = 2 (l + b) h = 2(3x + 2x) x = 10x2.
Now as Length gets doubled = 6x, Breadth halved = x, Height halved = x/2.
New area of four walls = 2 (6x + x) x/2 = 7x2.
Thus there is a decrease of 30%. Hence, fifth option is the answer.
Q2: A piece of string is 40 cm long. It is cut into 3 pieces. The longest piece is 3 times as long as the middle-sized piece & the shortest piece is 23 cm shorter than the longest piece. Find the length of the shortest piece (in cm).
Solution: This is the perfect question where options can be used to answer the question directly. If one considers option 3 i.e. 4 cm to be the length of the shortest piece then that means the longest piece should be of 27 cm and the middle sized piece can then found to be of 9 cm. Now the longest piece is clearly 3 times the middle sized piece and hence option 3 satisfies all the conditions and thus option 3 is answer.
Q3: 3 identical cones with base radius r are placed on their bases so that each is touching the other two. The radius of the circle drawn through their vertices is
1. < r
2. = r
3. > r
4. Depends on the height of the cone.
Solution: This is one of such questions where a student can get the answer based on his/her analyzing power and SYMMETRY depicted in the question.
Just try to visualize the three cones from their heads. The central point between the three is definitely at a distance, which is more than the radius; hence third option is the answer. Otherwise; just check if you have taken three equal circles who are touching the other two, the circle which will cover those three circles will be definitely the radius of the smaller circle plus something. Now it should be sufficient to conclude that it is more than r.
Q4: In the following figure the smallest cone has base radius 2 cm and height 1 cm. The heights of successive cones from the top form a G.P. with 1 as the first term and 2 as the common ratio. What shall be the ratio of the volumes of the smallest cone, to the two following frustrums?
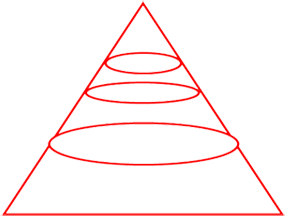
1. 1: 7 : 56
2. 1: 8 : 64
3. 3: 9 : 18
4. None of these
Solution: We get the heights of the successive cones as 1, 2 and 4. Since the base radii will increase in the same proportion as the heights, the volumes will be proportional to the cubes of the height (because volume = radius2 x height). So the ratio of the volumes will be 13 : 23 : 43 = 1 : 8 : 64. But the question is asking about the smallest cone to the frustum. Now the smallest cone has a volume of 1, the smaller frustum will have a volume of 7 (i.e. 8 – 1) and the bigger frustum will have a volume of 56 (i.e. 64 – 8). Thus the answer will be the first option.
Q5: A solid spherical ball is cut into eight identical pieces by three mutually orthogonal planes. The proportion the area of any of these pieces bears to the area of the uncut solid spherical ball is
1. 9/13
2. 11/16
3. 5/16
4. None of these
Solution: The spherical ball will have a surface area equal to 4πr2. The outer surface area of each of the smaller solid part will be 4πr2/8 ➾ πr2/2 and the inner part, which will look like one eighth of an orange will be quarter of a circle on left side, quarter of a circle on the right side and a quarter of a circle at the bottom as well. Opening it up you will get this as three-fourth of a complete circle. Thus this one piece will have a surface area equal to (πr2/2) + (πr2 × ¾). The total of this part will be 5/4πr2. This is what fraction of the original surface area i.e. 4πr2. This will give the ratio as 5/16. Thus 3rd option is the answer.

CAT Quantitative Aptitude: Preparation Articles

